Tá an modh chomh simplí agus sin, ach tá an luach ollmhór. Is é an eochair cibé acu a luachann tú é nó nach bhfuil!

Is é seo ach ceann de na modhanna, tá go leor modhanna níos mó a chuirfidh Jun Ge in iúl duit níos déanaí.

Is modh innealtóireachta cúltaca é léaráid conair uirlisí a tharraingt, agus cinnfidh cineál conair uirlisí conas scríobh an clár níos déanaí.

Mar shampla, taispeántar léaráid chonair ghearrtha snáitheanna sáraithe thíos, le honnaill deonach éagsúla ar an dá thaobh.

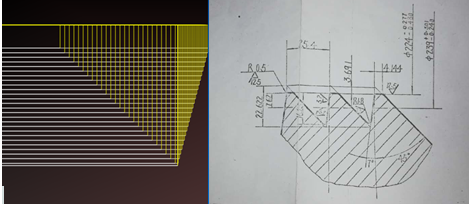
Mar shampla, léaráid chonair uirlisí le haghaidh snáite TR thíos, le huirlisí iasachtaithe ar an dá thaobh

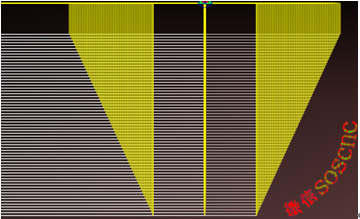
Labhróidh an t-alt inniu faoi mhacrachlárú le haghaidh snáitheanna i gcruth T

Mar a thaispeántar sa léaráid conair scian thuas: feithicil sraithe, trí scian in aghaidh an sraithe, is é sin, an lár ar dtús, agus ansin na scian ar chlé agus ar dheis ar an dá thaobh

Méadaigh an léaráid conair an scian mar a thaispeántar sa fhigiúr seo a leanas:

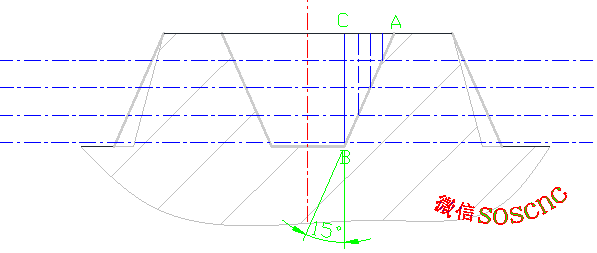
Ar an mbealach sin, is féidir le gach duine a fheiceáil go intuiciúil go mbeidh an t-uirlis ag gluaiseacht ar feadh líne AB mar thoradh ar an doimhneacht ghearrtha, ionas go dtiocfaidh an uirlis iasachtaithe amach leis an bpróifíl snáite is gá.

I bhfocail eile, tá caidreamh ann idir doimhneacht an scian X agus méid i dtreo Z, a shásaíonn an dlí Pythagorean, is é sin, TAN15=AC/BC

Mar sin, is féidir linn: AC=TAN15 * BC a bhaint amach

Tá an gaol seo ró- tábhachtach. Sa chlársceidealú ina dhiaidh sin, mar a athraíonn doimhneacht ghearrtha BC, athraíonn AC freisin de réir an gaol seo, agus mar sin próiseálann sé cruth na próifíle snáite de chineál Tr.

Mar sin, ní chiallaíonn cruth contúir Tr go bhfuil sé riachtanach go bhféadfar snáitheanna Tr a phróiseáil go sásúil.

Ós rud é gur gá uirlisí gearrtha a bhreithniú le linn próiseála freisin.

Ós rud é go bhfuil méid sonrach fiann ag gach snáithe de chineál Tr.

Mar shampla, is é leithead an lamhaigh roghnaithe 2mm (le haghaidh lamhaigh ar iasacht ar chlé agus ar dheis, ní mór leithead an lamhaigh a bheith níos lú ná leithead bhunúsach na fiann)

For example, TR100 * 12 external thread, the relevant dimensions are as follows:

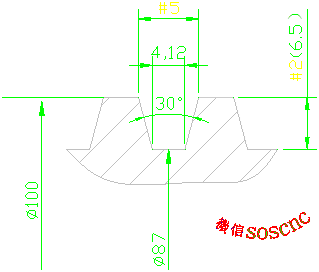
Is féidir liom aon líon athróg a shocrú mar a thaispeántar sa fhigiúr thuas

# 2 ionadaíonn airde na fianna, is é méid an bhriseadh

# 5 ionadaíonn leithead iomlán na ngionn, is é méid an phróifíl snáite a bhfuil gá againn a phróiseáil

# 5= 4. 12+2* TAN[ 15]*# 2

Ós rud é go bhfuil leithead ag uirlisí gearrtha freisin, ba cheart go mbeadh leithead iarbhír na calaoise alveolaire:

Leithead fothail an tanda+2×leithead an chlóige - leithead an uirlisí.

Mar sin, an deiridh # 5=4. 12+2 * TAN [15] * # 2- 2 (lena n- áirítear leithead an uirlis)

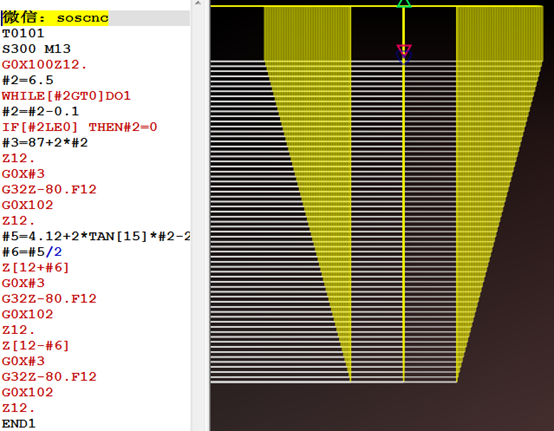
Go díreach go dtí an clár

T0101

S300 M13

G0X100Z12. (Bog go tapa go dtí tosphointe na snáite)

# 2=6. 5 (leithdháileadh tosaigh airde na fiann)

WHILE [# 2GT0] DO1 (Mura bhfuil airde na fianna tar éis 0 a shroicheadh, ciallaíonn sé nach bhfuil méid bhunúsach na snáite sroicheadh fós)

# 2=# 2- 0. 1 (méid gearrtha, 0. 1 in aghaidh sraithe feithicle, luach ar thaobh amháin)

IF[# 2LE0] THEN# 2=0

# 3=87+2 * # 2

Z12. (Is é Z12 an tagairt áitiúcháin, agus tá tosphointí na sciúin ar iasacht ar chlé agus ar dheis sa chlár ina dhiaidh sin bunaithe ar Z12)

G0X # 3 (gearrtha síos i dtreo X)

G32Z-80.F12 (gearrtha snáitheanna)

G0X102 (aisghabháil)

Z12. (Blad ar ais)

# 5=4. 12+2 * TAN [15] * # 2- 2

# 6=# 5/2 (ós rud é go bhfuil an scian ar iasacht ag an dá thaobh, roinn # 5 le 2 agus roinn sé ar an gcéanna)

Z [12+# 6] (An chéad scian a fháil ar iasacht ón taobh ceart, cuir # 6 leis toisc gur gá an scian bogadh chuig an deas)

G0X#3

G32Z-80.F12

G0X102

Z12.

Z [12 - # 6] (An chéad scian a fháil ar iasacht ón chlé, bain # 6 as mar is gá don uirlis bogadh chuig an chlé)

G0X#3

G32Z-80.F12

G0X102

Z12.

END1

G0X200.

Z200.

M30