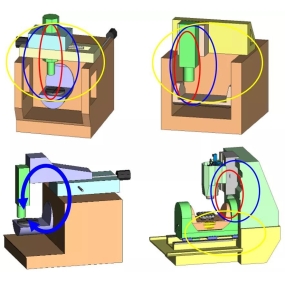
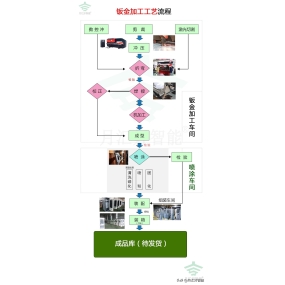
Analyse van plaatverwerking, assemblage en lasprocessen

plaatbewerking komt veel voor in de productie van de mechanische industrie en is een belangrijk onderdeel van de mechanische productie. Het heeft een breed scala aan toepassingen op gebieden zoals auto- en ruimtevaart. Het bepaalt direct het uiterlijk van de machine en weerspiegelt zijn rijpheid. Met de snelle ontwikkeling van de mechanische maakindustrie is de vorm van plaatmetalen onderdelen steeds complexer geworden. De berekening, buigen, lassen, spuiten en andere verwerkingsprocessen bij de ontwikkeling van metaalmaterialen bepalen direct of plaatdelen een goed uiterlijk, voldoende sterkte en de nodige nauwkeurigheid kunnen hebben. Daarom is het nauwkeurig berekenen van de ontvouwen grootte de primaire taak in plaatontwerp geworden, en plaatbuigen is een zeer belangrijk proces in plaatbewerking. De kwaliteit van het buigproces beïnvloedt direct de grootte en het uiterlijk van onderdelen, met name de kwaliteit van latere assemblage- en lasprocessen. Dit artikel analyseert de berekening van het vouwen van plaatmateriaal, buigproces, lassen, spuiten en andere processen vanuit het perspectief van technologie, gecombineerd met het werkelijke productieproces, en stelt oplossingen voor de problemen voor.

Alvorens te beginnen met het buigen, is het noodzakelijk om de afmetingen van elk onderdeel na het ontvouwen nauwkeurig te berekenen, evenals de positie van de sleuven of gaten op de tekening. Dit is om het probleem van het verschil tussen de gatpositie en de totale grootte op te lossen die wordt veroorzaakt door lasersnijden dat de tolerantie overschrijdt. Het externe materiaal zal verlengen onder het buigmoment van de interne metaalplaat, maar de lengte van de neutrale laag zal niet veranderen tussen spanning en compressie. Daarom is in het algemeen het berekenen van de ontvouwen lengte van plaatdelen equivalent aan het berekenen van de lengte van de neutrale laag. De werkelijke lengte van plaatcomponenten is de som van hun rechte lengte en neutrale laaglengte. De lengte van de karakteristieke laag is nauw gerelateerd aan het type, de dikte en de vorm van het gebruikte materiaal. Echter, in werkelijke verwerking, vanwege het feit dat de vorm en buigstraal van plaatmetalen delen hetzelfde zijn, is de berekening van buigstraal een eenvoudig algoritme zonder speciale vereisten, en de werkelijke grootte van buigstraal wordt in principe genegeerd. Hieronder is 90. Vereenvoudigde berekeningsmethode voor gebogen delen. De eenvoudige berekeningsformule is als volgt: L=d1+d2-a

Onder hen is L de gevouwen lengte, en d1 en d2 zijn 90. Bij het buigen zijn de twee rechthoekige randen van het onderdeel zijn totale grootte, en a is de buigcompensatiewaarde. Dit algoritme is geschikt voor de meeste buigende delen van plaatmetaal in plaatbewerking, vooral wanneer de buigende straal tussen 0.5mm en 2mm is en de plaatdikte minder dan 2.5mm is, is de berekening erg handig.

Echter, in de werkelijke productie en levensduur, in de meeste gevallen, is de buigcompensatiewaarde van plaatdelen onbekend. Op dit punt is het noodzakelijk om gebruik te maken van“ Testbuigen; Methode om de buigcompensatiewaarde te verkrijgen. De specifieke bewerking is als volgt: Gebruik eerst een werktuigmachine om twee vierkante materialen van gelijke grootte van de leverancier van het te testen materiaal te snijden, meet vervolgens nauwkeurig de afmetingen in beide richtingen en buig ze vervolgens in parallelle en loodrechte richtingen. Meet na het buigen de lengte van de twee rechte randen. Op dit punt is de buigcompensatiewaarde gelijk aan de lengte van twee rechte hoeken en de lengte van het oorspronkelijke vierkante materiaal, dat de compensatiewaarden van de grondstof in alle richtingen kan verkrijgen.